Posts 机器学习之基于交叉验证的特征选择
Post
Cancel

机器学习之基于交叉验证的特征选择

Feb 24, 2020 2020-02-24T04:21:00+08:00 on Machine Learning, Feature Selection

交叉验证通常用于模型选择，那么如何正确使用交叉验证进行特征选择呢？

交叉验证

模型在训练的时候往往是高方差估计. 从bias-variance tradeoff的角度看， 在有限数据的情况下训练的结果往往是bias较小但varance很大从而造成模型过拟合，因此降低了模型的泛化能力。为了在有限数据集的条件下使得模型尽可能满足泛化能力，提出了交叉验证 (Cross Validation, CV)，目的是增加模型训练的bias，降低variance, 从而在bias-variance tradeoff的角度上达到一定的平衡，提高模型的泛化能力。换句话说，交叉验证可以表征不同数据集的variance。

K-fold 交叉验证的一般步骤

交叉验证本质上是对给定的训练数据集进行切分。比如5-fold(即K=5)交叉验证的处理如下：首先将整个数据集等分为5份， 然后在一次轮迭代中使用第一等分用于模型训练过程中的验证集(validation set)， 剩下的4等份数据用于模型训练；第二轮迭代中使用第二等份作为验证集，剩下的用于模型训练，如此迭代5轮结束。

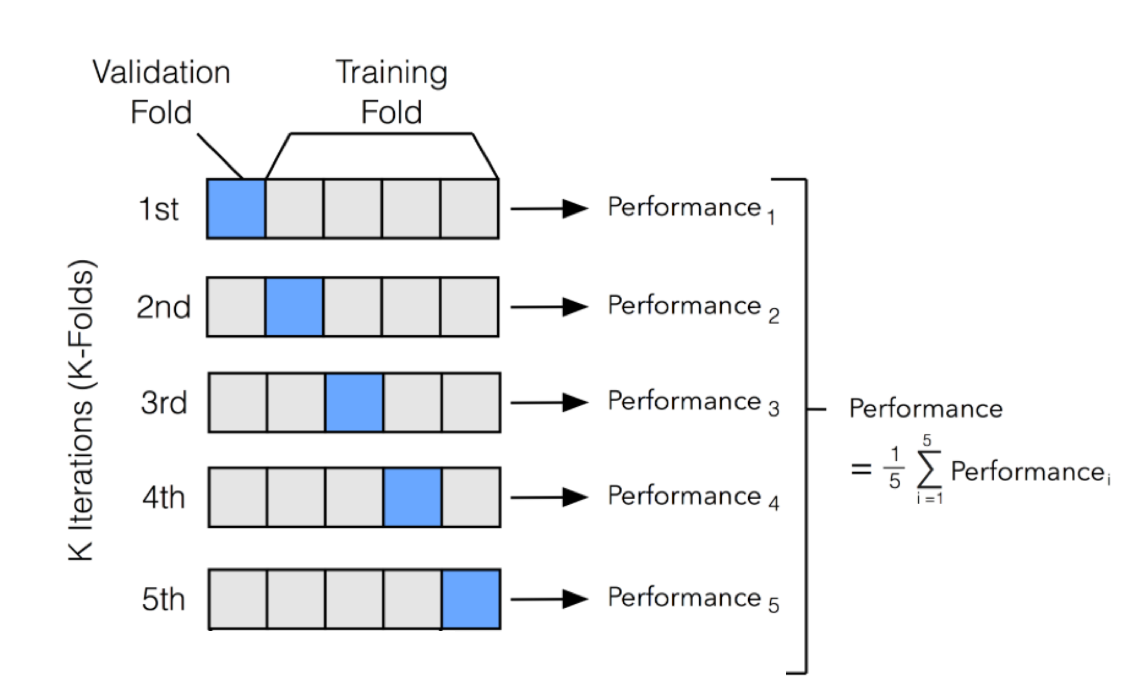5-fold cross validation 图一, 5-fold cross validation, image from here

例如用于模型最优参数选择（即模型选择）的伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# optional parameters list for a given type of model, eg, random forest
param_arr = ...

# splitting origianl whole training data
val_index, train_index = split_whole_training_data(whole_training_dataset)

# val_index and train_index are 5 element of array, and each element is also an array containing the index of i-fold validation dataset and training dataset, respectively.

pref_metrix=[]

for i_param in param_arr:

    i_param_perform = []
    for i_val_idx, i_train_idx in zip(val_index, train_index):
        i_val_data = whole_training_dataset[i_val_idx]
        i_train_data = whole_training_dataset[i_train_idx]

        # training model
        i_model = train(i_train_data)

        # evaluate model, like AUC, F1 and so on.
        preform_metrics = evaluate(i_model, i_val_data)
        i_param_perform.append(preform_metrics)
    
    # calculate mean value
    pref_metrix.append(mean(i_param_perform))

# finally, select the parameter according to the max pref_metrix.

以上是基于交叉验证的模型选择（也就是选择模型针对给定数据集的最有参数）的通用步(tao)骤(lu)。既然通过数据集切分的交叉验证表征了不同数据集的variance，那么就可以在这些切分后的数据集中找到一个在整体上使得模型预测的validation最小的“最优模型”，从而提高模型泛化能力。

交叉验证的姿势

那么如何通过交叉验证技术进行特征选择呢？它的过程是否与通过交叉验证技术进行模型选择一样呢？如果我们先在整个数据集上进行特征选择，然后再利用交叉验证进行模型选择，那么这样的过程是否是正确呢？是否人为的引入了偏差(bias)? 在回答这些问题前，我们先了解什么是数据泄漏(data leakage)。

数据泄漏 (data leakage)

在 PC 百科中对“数据泄漏”的定义为：

未经授权将机密信息从计算机或数据中心传输到外界。

那么对于交叉验证中的机密信息(the classified data in terms of cross validation)就是指测试数据集中的信息。这样测试数据集就可以看成是计算机或数据中心，而训练集可以看成是外界。换句话说，数据泄漏可以发生在模型从测试集和训练集进行学习的过程中。如果我们在交叉验证之外进行任何的数据预处理（比如特征选择，数据归一化等），我们将会对结果人为的引入bias，从而加大模型过拟合的风险。

回到刚刚提出的问题，如果我们先对整个数据集进行了特征选择（或predictor selection / variable selection）然后再通过交叉验证来评估模型性能（这个时候模型的性能将以均值($ \pm $标准差)的形式出现），那么最后的交叉验证的测试结果将会有偏差。换句话说，我们的k-fold交叉验证的准确性会被高估（即overfiting）。 （参考这里）

以下数据来自 Kaggle: https://www.kaggle.com/kumargh/pimaindiansdiabetescsv/data.

完整的代码可以移步到我的github.

交叉验证进行特征选择的错误姿势

先来看看交叉验证进行特征选择的错误姿势：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# 通过pandas来调用pearson correlation
kfold_score = []
# 5-fold cross validation 
kf = KFold(n_splits=5, shuffle=True, random_state=123)

for train_index, test_index in kf.split(np.arange(len(df_data))):
    
    # 对整个数据集进行特征选择 （错误的方式）
    # 使用pearson correlation
    cor = df_data.corr()
    #Correlation with output variable
    cor_target = abs(cor["Class"]).values
    #Selecting highly correlated features
    relevant_features = cor_target.argsort()[-5:][::-1]
    sel_feat_name = list(np.array(list(df_data.columns))[relevant_features])
    y = df_data['Class'].values
    sel_feat_name.remove('Class')
    print(sel_feat_name)
    sel_x_feat_dat = df_data[sel_feat_name].values
    
    x_train, x_test = sel_x_feat_dat[train_index], sel_x_feat_dat[test_index]
    y_train, y_test = y[train_index], y[test_index]
    
    # 预测
    clf = LogisticRegression(random_state=0, solver='liblinear', max_iter=200).fit(x_train, y_train)
    kfold_score.append(clf.score(x_test, y_test))
    
kfold_score_arr = np.array(kfold_score)
print('5-fold sorce: {}'.format(kfold_score_arr))
print('avg score: {}'.format(np.mean(kfold_score_arr)))
  1. 首先构建5-fold的交叉验证集（集训练集合测试集）；
  2. 其次，基于最大相关系数选择最相关的特征。
  3. 使用选出的4个特征的训练集训练逻辑回归模型，并在测试集上计算模型的准确率。

可以看出，我们使用的是整个数据集（训练集+测试集）计算相关系数，然后选择相对于response variable相关性最大的4个特征。

但是这样做是错误的，我们应该在训练集上进行特征选择（计算相关系数）而不碰测试集。

由于我们使用完整数据集进行特征选择，所以在交叉验证的每一次循环中选择的特征都是一样的，这就是使用交叉验证进行特征选择普遍出现的错误，下面是输出：

1
2
3
4
5
6
7

['Glucose', 'BMI', 'Age', 'Pregnancies']
['Glucose', 'BMI', 'Age', 'Pregnancies']
['Glucose', 'BMI', 'Age', 'Pregnancies']
['Glucose', 'BMI', 'Age', 'Pregnancies']
['Glucose', 'BMI', 'Age', 'Pregnancies']
5-fold sorce: [0.77272727 0.75974026 0.7012987  0.78431373 0.78431373]
avg score: 0.7604787369493251

在The wrong way and the right way to do cross-validation 中已经明确说明： 这样错误的方式进行交叉验证会显著的低估真正的错误率(error)。

交叉验证进行特征选择的正确姿势

正确的做法是，在进行特征选择的时候（也就是计算相关系数的时候）我们不使用整个数据集。相反，在交叉验证的每次循环中使用训练集进行特征选择。这样在每次进行特征选择时所使用的数据集不同，那么每次循环选择的特征列表页可能不一样：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# 通过pandas来调用pearson correlation
kfold_score = []
# 5-fold cross validation 
kf = KFold(n_splits=5, shuffle=True, random_state=123)

for train_index, test_index in kf.split(np.arange(len(df_data))):
    
    # 对整个数据集进行特征选择 （错误的方式）
    # 使用pearson correlation
    train_df = df_data.iloc[train_index, :] 
    test_df = df_data.iloc[test_index, :] 
    
    cor = train_df.corr()
    #Correlation with output variable
    cor_target = abs(cor["Class"])
    #Selecting highly correlated features
    relevant_features = cor_target.argsort()[-5:][::-1]
    sel_feat_name = list(np.array(list(df_data.columns))[relevant_features])
    y = df_data['Class'].values
    sel_feat_name.remove('Class')  
    
    print(sel_feat_name)
    
    x_train, x_test = train_df[sel_feat_name].values, test_df[sel_feat_name].values
    y_train, y_test = y[train_index], y[test_index]
    
    # 预测
    clf = LogisticRegression(random_state=0, solver='liblinear', max_iter=200).fit(x_train, y_train)
    kfold_score.append(clf.score(x_test, y_test))
    
kfold_score_arr = np.array(kfold_score)
print('5-fold sorce: {}'.format(kfold_score_arr))
print('avg score: {}'.format(np.mean(kfold_score_arr)))

输出结果如下：

1
2
3
4
5
6
7

['Glucose', 'BMI', 'Age', 'SkinThickness']
['Glucose', 'BMI', 'Age', 'Pregnancies']
['Glucose', 'BMI', 'Age', 'Pregnancies']
['Glucose', 'BMI', 'Pregnancies', 'SkinThickness']
['Glucose', 'BMI', 'Age', 'Pregnancies']
5-fold sorce: [0.76623377 0.75974026 0.7012987  0.79084967 0.78431373]
avg score: 0.7604872251931075

可以看出，每次循环选择的特征列表并不相同。那么新的问题来了：每次循环的特征都是不一样的，我们应该怎么选择呢？答案是对每一个特征使用最大投票 majority voting。 比如上面结果中，我们最终使用的特征列表是 ['Glucose', 'BMI', 'Age', 'Pregnancies']， 这些特征在交叉验证的5次循环中分别出现的次数是：5， 5，4，4.

以上才是交叉验证进行特征选择的正确姿势。需要注意的是，这里使用的交叉验证只是进行了特征选择，没有进行模型选择。如果需要进行模型选择，还要在每个交叉验证的循环中，在完成特征选择后再进行模型选择。 总的来说，每个交叉验证循环内的处理过程是：交叉验证生成训练集和测试集->基于训练集进行特征选择->特征选择后的训练集进行模型训练（如果需要模型选择，就在这个部分进行）->使用特征选择后的测试集评估模型。

注意， 特征必须要进行scale，否则1：经典机器学习中，特征值的很大会dominate特征值小的特征 2、深度学习中，梯度沿着特征值大的方向下降的比特征值小的快，影响训练。

哪些预处理可以先用交叉验证前完成？

凡是可以基于单一样本进行数据处理的预处理都可以在交叉验证循环外进行，比如数据清理，数据平滑等只要不影响其他样本的处理都可以在交叉验证循环外进行。

如果预处理是样本批量进行，那么这样的预处理就必须在交叉验证循环内进行，比如中心化(centering即使得均值为0)，归一化/标准化(StandardScale)，特征选择等。

换句话说(查看这里):

只有当所有与模型训练相关的各个方面的处理在交叉验证的循环中进行时才能说明交叉验证是非偏向性的(unbiased)。这些与模型训练相关的处理包括：特征选择，模型选择，模型参数微调（parameter）等。

代码：https://github.com/y-bai/machine-learning/blob/master/cross-validation-feature-selection.ipynb

Feature Selection Cross Validation Pearson Correlation
This post is licensed under CC BY 4.0

-

组学之游离DNA

Comments powered by Disqus.