什么是最优传输理论?
最优传输理论(Optimal transport, OT)最早是Monge于1781年提出。假设有多个“土堆”及多个“坑”,OT要解决的问题是找到最优(代价最小)的运输方案将土堆用来填满每个这些坑。另一个应用场景是“土堆”对应货物仓库,“坑”对应不同的购物消费者。
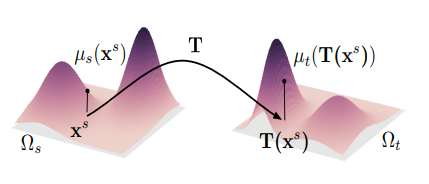
Figure from Optimal Transport for Domain Adaptation, 其中$\Omega_s$是起点质量空间, $\mu_s(\mathbf{x}^s)$ 是起点位置 $\mathbf{x}^s$ 的质量,$\mathbf{T}$是传输方案, $\mathbf{T}(\mathbf{x}^s)$是起点 $\mathbf{x}^s$ 经过传输 $\mathbf{T}$ 后的终点位置,$\mu_t(\mathbf{T}(\mathbf{x}^s))$是终点位置的质量。
OT是对不同概率分布之间“距离”的一种度量。距离函数的两个理想属性是对称性(symmetry)和三角不等式(triangle inequality)。不幸的是,概率分布之间的许多“距离”概念并不满足这些属性。这些较弱的距离概念通常称为"散度(divergence)"。比如最著名的Kullback-Liebler (KL) 散度:
犹如我们相见的KL散度也是一种描述概率分布之间相似性的一种度量。那为什么不用KL呢?主要是因为KL只能比较support相同的概率分布。什么是support呢?
http://alexhwilliams.info/itsneuronalblog/2020/10/09/optimal-transport/
sup是单词supremum的简写,意思是最小上界(上确界)。inf是单词infimum的简写,意思是最大下界(下确界)。
https://mathematical-coffees.github.io/slides/mc01-courty.pdf https://zhuanlan.zhihu.com/p/94978686
https://www.zhihu.com/question/55198447
https://www.jiqizhixin.com/articles/2018-10-04-3
https://www.jiqizhixin.com/articles/2018-10-04-3
https://mathematical-coffees.github.io/mc01-ot/
参考
- http://alexhwilliams.info/itsneuronalblog/2020/10/09/optimal-transport/
- https://medium.com/analytics-vidhya/introduction-to-optimal-transport-fd1816d51086
https://zhuanlan.zhihu.com/p/82424946
https://icerm.brown.edu/topical_workshops/tw-23-otds/
https://michielstock.github.io/posts/2017/2017-11-5-OptimalTransport/ https://dfdazac.github.io/sinkhorn.html
https://github.com/iamalexkorotin/NeuralOptimalTransport
https://zhuanlan.zhihu.com/p/573158960
https://www.kernel-operations.io/geomloss/_auto_examples/index.html
https://medium.com/intuitionmachine/optimal-transport-theory-the-new-math-for-deep-learning-2520395fc183